Overlapping intervals in real life

Prelude

Ever encountered a Leetcode problem in your day-to-day?

You know, those algorithmic problems you had to grind for days on end, just to fail the FAANG (or MAANG, GAMMA, take your pick) interview because someone else did it 10 seconds faster?

Roman literals to integer, coin change, tree traversal, merge intervals; or problems where binary search is usually the answer?

Hate them or love them, they are reality nowadays.

And for those that love them and especially for those that hate(d) them, here I am to say: it was not all in vain!

It has finally happened: I have encountered one in the wild.

Scenario

Processing data in a Kubernetes cluster using Airflow to orchestrate. Match made in heaven, right?

Until you are told you have limited resources. No, you cannot just keep asking for more, nor can the usage spike over a low… very low limit.

So low, that besides decommissioning datasets, the only option left is to optimize the schedules such that your limited resources are never on standby; they have to work 24/7.

Wait, isn’t Airflow supposed to optimize that for you?

There is actually a great summary here by one of the Airflow contributors as to why this is will never happen.

Can’t you just limit the slots?

Yes, and you probably should configure reasonable pool sizes. However that does not take into account the resources required by a given task. One could very well say “I have 10GB of memory, most of my tasks need 2GB, let’s set a pool of 5”, only to realize that those few remaining tasks that require 6GB of memory each could trigger at the same time.

What about limiting the number of tasks in parallel within a DAG?

Yes, setting max_active_tasks is definitely important, especially in DAGs with a lot of parallelizable tasks. However just like with pools, it does not take into consideration the resources requirements. Keep this config option in mind though!

What about task retries?

Yes, can also set up retries such that if the Kubernetes cluster is out of resources, Airflow just tries again a bit later hoping that there will be enough resources available at the next attempt. However in reality this could easily lead to tasks being starved for hours just because whenever they are retried, it just so happens that other tasks have already taken those slots / resources. Business would not be very happy that their dashboards are randomly not up-to-date during their important apéro’s cough meetings.

But enough questions for now!

In all of these cases, one can of course just turn a blind eye and say: hey, you want this better, give us more resources!

But wouldn’t that be rather boring? What if we could just shift the schedules a bit and minimize the effects of the drastically limited resources? Surely there is a way to do this!

ChatGPT?

Problem Statement

Let’s be analytical about it.

We already have “hard” coded DAGs, their tasks, and most importantly, their schedules, which means we know when they should start. We also have historical data about their runtimes in the airflow metadata db. This means we could plot a graph of the expected durations, which could look like:

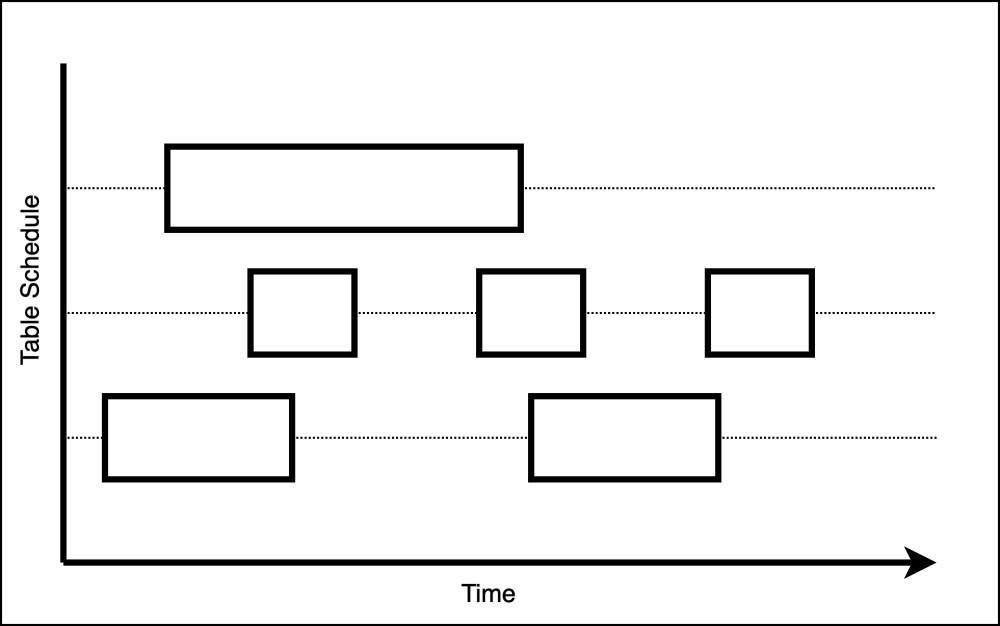
And if looking at the resource usage, that could (very roughly) look like:

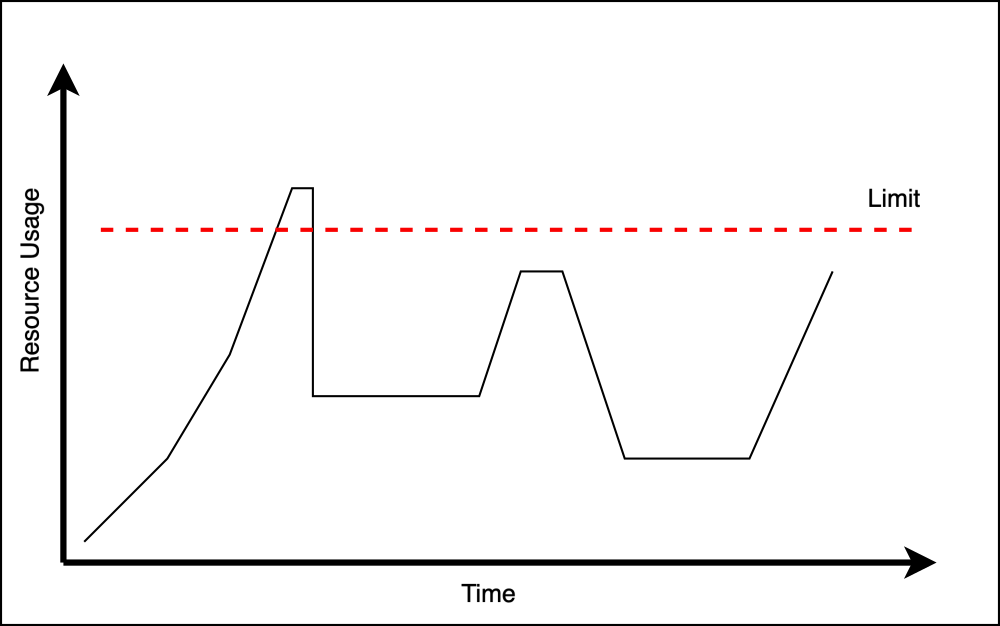
So we can visualize the expected duration of each DAG over time and at which points we would exceed the limits of our system. Couple that with information about the resources required by the tasks within DAGs, plus the maximum available resources in your cluster, and we could write some algorithm to check whether at any point we ask for more resources than we can handle - before the fact.

This is important. The whole point here is not to try random configurations, deploy those changes, analyze, rinse and repeat. We want to do this sort of analysis “statically”, so just within the code and thus without any deployments.

Heck, the algorithm could even spew out the biggest gaps and recommend how to shift these schedules.

But let’s not get ahead of ourselves.

We want to find the moments in time when we likely request more resources than available.

So look at the previous image again. Those are essentially intervals, and we are looking for overlaps.

Does it ring a bell?

Leetcode

Medium Leetcode indeed! Or more like a variation of it. Perhaps a more difficult one. Is this maybe a Hard Leetcode?

Let’s first make it more Leetcode-y:

Given

• an array of arrays of tuples intervals where intervals[i] = [tuple_i, tuple_i+1, ...] and tuple_i = [start_timestamp, end_timestamp],
• a mapping of intervals to resources interval_to_resources where interval_to_resources[i] = float
• a maximum float limit of resources limit

Merge and return the intervals where the sum of resources exceeds the limit.

(Simplified) Example:

Input:
intervals = [[[0, 2], [4, 6]], [[1, 3], [5, 7]]]
interval_to_resources = {0: 2.0, 1: 3.0}
limit = 4.0

Output: [[1, 2], [5, 6]]
Explanation: Those are the overlaps in the intervals where the sum of resources would exceed the limit.

Ideas?

Code

Of course there is a brute force option, then a more optimized approach. First however, we are talking about a real use case. So before we reach the algorithm phase, some code to actually compute the things we need. Essentially let’s prepare the Input.

I will be using polars for simplicity.

The source data:

from datetime import datetime

import polars as pl

execution_logs = pl.DataFrame([
  ["table1", "succeeded", datetime(2025, 1, 1, 0, 0), datetime(2025, 1, 1, 0, 5)],
  ["table1", "failed", datetime(2025, 1, 1, 0, 15), None],
  ["table1", "succeeded", datetime(2025, 1, 1, 0, 30), datetime(2025, 1, 1, 0, 40)],
  ["table2", "succeeded", datetime(2025, 1, 1, 2, 0), datetime(2025, 1, 1, 2, 30)],
], schema=["table", "status", "start_ts", "end_ts"], orient="row")

table_schedules = pl.DataFrame([
  ["table1", "@hourly"],
  ["table2", "5 * * * *"],
], schema=["table", "schedule"], orient="row")

table_resources = pl.DataFrame([
  ["table1", 1],
  ["table2", 2.5],
], schema=["table", "memory"], orient="row")

available_resources = 3.0

Indeed, this is still a bit simplified. In reality, the execution logs would come from the Airflow db, the table schedules and resources would be extracted from the DagBag, and the available resources would likely contain both cpu and memory.

But let’s stick to the fun parts.

We then compute the mean durations:

mean_durations = (
  execution_logs
  .filter(pl.col("status") == "succeeded")
  .with_columns(duration=pl.col("end_ts") - pl.col("start_ts"))
  .select("table", "duration")
  .group_by("table")
  .agg(pl.mean("duration").alias("mean_duration"))
)

Then some functions to generate the intervals:

from datetime import timedelta

def generate_expected_runtime_intervals(
  first_datetime: datetime,
  delta_to_next_trigger: timedelta,
  mean_duration: timedelta,
  min_frequency: timedelta
):
  assert mean_duration < delta_to_next_trigger, f"Cannot have overlapping intervals!"
  start_times = (
    pl.datetime_range(
      first_datetime,
      first_datetime + min_frequency,
      timedelta_to_polars_interval(delta_to_next_trigger),
      eager=True
    )
  )
  end_times = start_times + mean_duration

  return list(zip(start_times, end_times))

Indeed glossing over some details, such as converting from those schedule expressions @hourly or cron 5 * * * * to timestamps and deltas. The full (yet still simplified!) code will indeed be available in the repo.

Note however the min_frequency_days parameter. This is essentially to configure how long into the future we want to compute intervals for, which should actually be the least-frequent schedule in our input data. This could be weekly, or perhaps even monthly. Going any further might be a bit unrealistic or uncommon, but still relevant to this exercise, as we shall see!

Leetcode time

Now you might be wondering how to proceed, and perhaps already noticed that we deal with datetime’s, not integers, in the intervals. In a way, it is like going from integers to floats. How do we find the overlaps now?

Also note how the problem is not to simply merge the intervals - in which case we would likely just have a single long one in the end - but to find the places where they overlap and the resources exceed a certain limit.

I know! I know!

The analytical side is likely excitingly shouting that we could try a sort of “sample” frequency. Say we “poll” these intervals at the figurative tick of the clock and compute the expected resource usage then. We won’t do this every second; that would be overkill. Let’s say we check every 30 seconds.

Isn’t this approach ‘cheating’? There could be overlaps we will miss!

Perhaps it is. However this is where the realism comes into play. Does our data really have schedules starting at odd times, such as 02:34:57?

No! Most schedules would be at round numbers, since who doesn’t like that.

And this parameter is configurable after all. Could be every couple of seconds, or even every half hour. The best thing is that it could also be statically inferred from the schedules!

And if we only have cron schedules, it is actually decided for us, as the smallest unit is a minute.

Ok ok, let’s see some code!

def generate_polls(
  from_datetime: datetime,
  duration_to_check: timedelta,
  frequency: timedelta
) -> List[datetime]:
  return pl.datetime_range(
    from_datetime,
    from_datetime + duration_to_check - frequency,
    frequency,
    eager=True
  )

We have duration_to_check which should match the min_frequency_days, and the frequency which is the polling interval, such as every 30 seconds.

And some final preparation before the actual algorithms:

table_to_intervals = {
  table: generate_expected_runtime_intervals(
    schedule_to_first_datetime(schedule),
    schedule_to_delta_next_trigger(schedule),
    # default if no previous execution (recorded)
    table_to_mean_duration.get(table, timedelta(minutes=10)),
    timedelta(days=30)
  )
  for table, schedule in table_to_schedule.items()
}

tables = list(table_to_intervals.keys())
intervals = table_to_intervals.values()

def interval_contains_datetime(interval: Tuple[datetime, datetime], poll: datetime) -> bool:
  return poll >= interval[0] and poll <= interval[1]

Brute force

def compute_estimated_resource_usage_brute_force(
  intervals: List[List[Tuple[datetime, int, str]]],
  duration_to_check: timedelta,
  frequency: timedelta
) -> List[Tuple[datetime, float, str]]:
  polls = generate_polls(datetime(2025, 1, 1), duration_to_check, frequency)

  result = list()
  for p in polls:
    resources = 0
    tables_involved = list()
    for ii, table_intervals in enumerate(intervals):
      for interval in table_intervals:
        if interval_contains_datetime(interval, p):
          resources += table_to_resources[tables[ii]]
          tables_involved.append(tables[ii])
    result.append((p, resources, tables_involved))

  return result

Which would essentially be used like:

result = compute_estimated_resource_usage_brute_force(intervals, duration_to_check=timedelta(hours=6), frequency=timedelta(seconds=30))
filtered_result = (r for r in result if r[1] > available_resources)
print(any(filtered_result))

To find out whether we ever exceed the limits.

And what is the complexity, you say?

Well for each poll, we iterate over all the schedules (lists of intervals), and for each schedule we iterate over all the intervals interval. We check if the poll is within the interval, and if yes, keep track of it and the associated table and resources required.

So the complexity is O(num_polls * num_schedules * num_intervals), with the asterisk that each schedule might have a different number of intervals; still, somewhere between to the power of 2 and to the power of 3.

Not that nice.

Many pointers

def compute_estimated_resource_usage_pointers(
  intervals: List[List[Tuple[datetime, int, str]]],
  duration_to_check: timedelta,
  frequency: timedelta
) -> List[Tuple[datetime, int, str]]:
  polls = generate_polls(datetime(2025, 1, 1), duration_to_check, frequency)
  result = list()
  pointers = [0 for _ in range(len(intervals))]
  lengths = [len(table_intervals) for table_intervals in intervals]

  def compare(interval: Tuple[datetime, datetime], poll: datetime) -> int:
    if interval_contains_datetime(interval, poll):
      return 0
    elif poll > interval[1]:
      return 1
    else:
      return -1

  for poll in polls:
    resources = 0
    tables_involved = list()
    for interval_index, table_intervals in enumerate(intervals):
      if pointers[interval_index] >= lengths[interval_index]:
        continue

      comparison = compare(table_intervals[pointers[interval_index]], poll)
      if comparison == 0:
        resources += table_to_resources[tables[interval_index]]
        tables_involved.append(tables[interval_index])
      elif comparison > 0:
        pointers[interval_index] += 1
      elif comparison < 0:
        pass
    result.append((poll, resources, tables_involved))

  return result

What is the complexity here then?

We do use some extra space to keep track of pointers and the number of intervals, however this is negligible. Computationally however, we essentially loop in parallel over the intervals. So we still iterate over the polls, and for each poll over the schedules, however we keep track of the intervals we have already been through as we go along. This means we effectively placed our algorithm somewhere between the power of 1 and the power of 2; much better!

Can you spot some issues with the algorithm though?

Indeed there are!

First, it assumes that the intervals (so from the expected start time for the average duration) is not smaller than the polling frequency.

Secondly and perhaps as a corollary, if the intervals overlap, it would also not work! Arguably this would point to bigger issues in the orchestration setup; nevertheless, it is also easy to prevent (or at least check).

See if you can spot where exactly the code would fail in these scenarios ;)

Profiling

We have all seen the classical plot with the complexities; how about we make it practical?

Let’s stress test these algorithms!

Use an arguably long duration of 30 days and a polling frequency of 30 seconds. This means we’d have roughly 30 * 24 * 60 * 2 = 86400 polls and 2 * 30 * 24 = 1440 intervals.

import timeit

duration = timedelta(days=30)
frequency = timedelta(seconds=30)

brute_time = timeit.timeit(lambda: compute_estimated_resource_usage_brute_force(intervals, duration, frequency), number=10)
pointers_time = timeit.timeit(lambda: compute_estimated_resource_usage_pointers(intervals, duration, frequency), number=10)
print(f"brute_force={brute_time:.3f}s, pointers={pointers_time:.3f}s")

Which gives us

brute_force=55.243s, pointers=0.497s

A roughly 110x improvement with the pointers approach!

And this is only with 2 schedules for a single month; in reality we’d have 100s of schedules.

Leetcode is not that bad now, is it?

Summary

So was this realistic?

Well in our case, this is stretching it a bit.

In a real Airflow setup, one would likely use pools and configure max_active_tasks. This means tasks might not actually start at the scheduled time, but some time later. While still possible to estimate with data from the airflow db, which does store task start and finish times (not just for whole DAGs), it does introduce an extra layer of uncertainty. So the start times could be for example between 0 and 15 minutes past the scheduled time.

The cron expressions could also be more complex, such as with fractions or at specific minutes during an hour, which the code in the blogpost cannot currently handle. Nevertheless, this would be “just” a problem of parsing the cron expressions, and generating the intervals correctly; not of the algorithms we wrote!

And of course there could be other variables, such as the Kubernetes cluster being used by other parties and hogging the resources, be this an irregular occurrence or not.

Nevertheless, the challenge was definitely interesting to (at least partially) solve! We have seen how Leetcode-level technical challenges could pop up in our day-to-day, even if seldomly.

And hopefully, one can find some joy in these sort of challenges away from the usual grind.

Addendum

Why not just check metrics and plots of resource usage?

Those come after the fact, so one would adjust, deploy, wait for schedules to pass, and observe if there are still issues. This would generally work, don’t get me wrong! However the scenario here is dealing with tightly constrained resources and a demand to be both efficient and fast. This means being able to “simulate” scenarios, i.e. schedule shifts, before actually spending the time to deploy. For those in corporate, you know well how long these deployments could take and the amount of “paperwork”.

Hey, you left us hanging with those issues in the pointers algorithm!

And I will continue to do so :) Take it as a challenge from The Engineer.

I know a better solution!

There probably are alternatives. Do contribute to the discussion!